Manipulating Math with Formula Morph

Posted on April 21, 2015 by Experiment Station

Trying out Formula Morph in the Man Ray–Human Equations exhibition

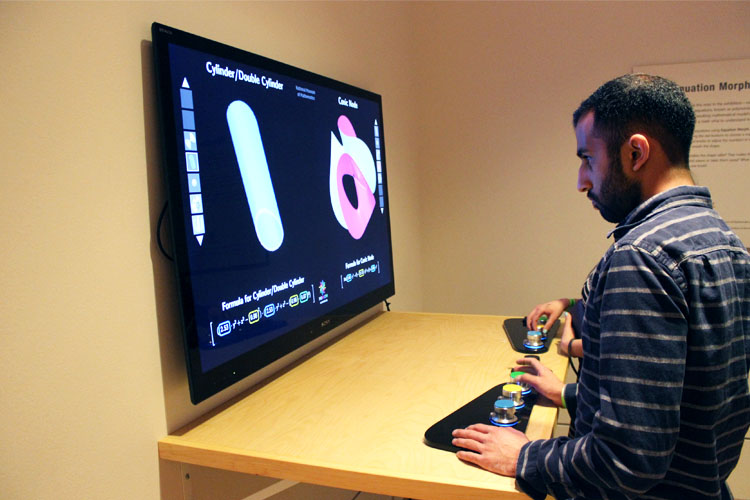
Man Ray–Human Equations showcases Man Ray’s depictions of complicated mathematical objects that he first encountered in the 1930’s. The models served as educational tools for mathematical students; however, Man Ray was interested in how they looked more than the specific mathematical equations they represented. Because the equations are fairly complicated and dense, The Phillips Collection incorporates a participatory experience, Formula Morph, into the exhibition to help visitors better understand the visual representation of the equations.

Provided by the Museum of Mathematics in New York City, Formula Morph shows some of the same models and equations that are featured in the exhibition. Users can select an equation, and adjust it using colored knobs that then alter the shape of the object on the screen. Formula Morph creates a visual connection between the objects Man Ray used with the complicated mathematical equations that they represent.

Kelley Daley, Graduate Intern for Programs and Lectures

Visitors adjust colored knobs to alter the mathematical models on the screen.

Man Ray’s Shakespearean Equations: Merry Wives of Windsor

Posted on April 13, 2015 by Experiment Station

Merry Wives of Windsor_mathematical model pairing

(left) Man Ray, Shakespearean Equation, Merry Wives of Windsor, 1948. Oil on canvas, 24 x 18 1/8 in. Private Collection, Courtesy Fondazione Marconi, Milan. © Man Ray Trust / Artists Rights Society (ARS), NY / ADAGP, Paris 2015 (right) Mathematical Object: Imaginary and Real Part of the Derivative of the Weierstrass ℘–Function, c. 1900. Plaster, 6 1/2 × 8 × 5 7/8 in. Brill-Schilling Collection. Institut Henri Poincaré, Paris. Photo: Elie Posner

Man Ray explained that the mathematical model of an elliptical function in this Shakespearean Equation reminded him of “the group of merry wives of Windsor getting together to gossip and laugh.” A former Phillips intern remarked that the artist’s dash of color in his interpretation of this mathematical model really does make it merrier.

Man Ray’s Shakespearean Equations: Julius Caesar

Posted on April 6, 2015 by Experiment Station

Julius Caesar_mathematical model pairing

(left) Man Ray, Shakespearean Equation, Julius Caesar, 1948. Oil on masonite, 24 × 19 3/4 in. The Rosalind & Melvin Jacobs Collection, New York. © Man Ray Trust / Artists Rights Society (ARS), NY / ADAGP, Paris 2015 (right) Mathematical Object: Real Part of the Function w=e, c. 1900. Plaster, 9 × 12 3/8 × 7 1/2 in. Brill-Schilling Collection. Institut Henri Poincaré, Paris. Photo: Elie Posner

Julius Caesar epitomizes Man Ray’s inventive approach to humanizing and translating mathematical models into enigmatic forms in his Shakespearean Equations series. In this composition (at left), he mapped out the undulating lines defining the model, creating a headless torso and casting the transformed object as the central character in a theatrical tableau. Note on the blackboard behind the imposing form barely discernable mathematical equations such as “2 + 2 = 22.” These seemingly illogical mathematical notations embed further mystery in Man Ray’s characteristically enigmatic manner. In the space between two relational formulations on the blackboard the artist posed the philosophical question and unsolved problem of the “square root of Man Ray.” The answer to and meaning of this conundrum is left for us to decipher for ourselves.

Of his Shakespearean Equations, Man Ray once stated “In painting [the models], I did not copy them literally but composed a picture in each case, varying the proportions, adding color, ignoring the mathematical intent, and introducing an irrelevant form sometimes, as a butterfly or the leg of a table.” In his rendering of Julius Caesar, he recycled the table leg employed in his 1945 object Obelisk see Oculist (Pied à terre) to evoke the scepter of a triumphant general.

Do you see anything else in this painting that might evoke Shakespeare’s Julius Caesar?

Wendy Grossman, Exhibition Curator